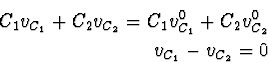|
Consider the electrical circuit in Fig. 5. When the switch, Sw, is open, the parallel RLC circuit on its right exhibits damped oscillatory behavior and both the energy storing elements, C2 and L are independent. When the switch is closed, vC2 is forced to equal vC1 which may call for an instantaneous redistribution of charge between C1 and C2 based on the conservation principle. The inductor, L, remains independent, and, therefore, does not partake in the state redistribution.
The system of
equations that describes the behavior after the switch is
closed can be compiled as
![\begin{displaymath}
\left.\begin{array}
{c}
\left[\begin{array}
{ccccc}
1 & 0 & ...
...\ i_L \\ i_{C_1} \\ i_{C_2}\end{array}\right]\end{array}\right.\end{displaymath}](img57.gif)
The algebraic constraint in the equation on the bottom row captures
the voltage dependency between the two capacitors C1 and C2.
The equation on the one but last row describes the nodal equation that
all currents sum to . These two equations form h.
The first three rows form the equations that
capture the time-derivative constituent
behavior of C1, C2, and L1, and are part of f.
Therefore,
![\begin{displaymath}
\dot{\bar{x}} =
\left[\begin{array}
{c}
\dot{v}_{C_1} \\ \do...
...eft[\begin{array}
{c}
v_{C_1} \\ v_{C_2} \\ \end{array}\right].\end{displaymath}](img58.gif)
The remaining variable and its derivative are not part of algebraic
constraints, and, therefore, continuous. They belong to
![]()
The equation on the bottom row contains algebraic contraints in x only,
and forms ![]() . The equation on the one but last row contains
the algebraic variables
. The equation on the one but last row contains
the algebraic variables
![\begin{displaymath}
\hat{y} =
\left[\begin{array}
{c}
i_{C_1} \\ i_{C_2}\end{array}\right].\end{displaymath}](img60.gif)
Partitioning F and H results in
![\begin{displaymath}
F' =
\left[\begin{array}
{cc}
\frac{1}{C_1} & 0 \\ 0 & \fra...
... \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & -\frac{1}{L}\end{array}\right]\end{displaymath}](img61.gif)
and
![\begin{displaymath}
\hat{H}' =
\left[\begin{array}
{cc}
0 & 0 \\ 1 & 1\end{arra...
...-\frac{1}{L} & 0 & 0 \\ -\frac{1}{R} & 0 & -1\end{array}\right]\end{displaymath}](img62.gif)
From this, the pseudo-inverse of F' is
![\begin{displaymath}
F'^+ =
\left[\begin{array}
{ccc}
C_1 & 0 & 0 \\ 0 & C_2 & 0\end{array}\right]\end{displaymath}](img63.gif)
Therefore,
![\begin{displaymath}
\hat{H}' F'^+ F'' =
\left[\begin{array}
{cccc}
0 & 0 & 0 & 0 \\ C_1 & C_2 & 0 & 0\end{array}\right]\end{displaymath}](img64.gif)
which results in the projection equation based on conservation
principles (Eq. (22))
![]()
Given Eq. (8) through (10),
the right-hand terms
are for ![]() . The remainder can be written as
(v = v(t+) and v0 = v(t-))
. The remainder can be written as
(v = v(t+) and v0 = v(t-))
![]()
Along with the algebraic
equations, ![]() , this yields the system of equations
, this yields the system of equations